Solving substitution ciphers with genetic algorithms

After writing my "Solving substitution ciphers" post, I started wondering whether the same problem could be solved using a genetic algorithm. It turns out that genetic algorithms only partly work for this problem (at least in their simplest form), but they do work well enough to show some of the benefits of the technique.

As usual, my process for trying this out was to basically glance at the Wikipedia page and see where I could go from there. Based on my glancing, I discovered that to solve an optimisation problem with a genetic algorithm, you need two things:

• A way to represent a candidate solution as a string or array
• A way to score each candidate, i.e. a 'fitness' function

As a very simple example, let's say you want to find three digits $a, b, c$ that maximise the function $f(a, b, c) = a * b - c$. Each candidate solution would just be a string like "524"

"Breeding" solutions

To solve a problem with a genetic algorithm, you first generate a population of potential solutions. In our very simple example, these could just be 10 strings of random digits like "315", "824", etc. Then you score each solution - here the score for each string abc could just be f(a, b, c): 315 scores -2 and 824 scores 12.

Once you have a population and some fitness scores, you can take some of the top solutions and breed them together: you might just select the top two solutions from every generation. The main way we'll breed new solutions is with crossover: take two solutions, pick a random point along their length, and take everything on one side of the crossover point from one solution, everything else from the other. With our simple example of 315 and 824, we could do:

Parent 1:        3 1 5
Parent 2:        8 2 4
Crossover point:    ^
Child:           3 1 4

We breed a new population of 10 new strings from our selected solutions, and repeat until we've solved the problem (or scores are no longer improving etc.)

Genetic algorithms for cipher solving

It seemed like there should be a straightforward way to apply genetic algorithms to a substitution cipher:

• Each possible key can be thought of as a 26-character string like cfwrdvhilojztybkeqnsaumpxg, where a is substituted for c, b for f and so on.
• The fitness function is the log-likelihood based on letter and bigram frequencies that I used in the previous cipher solving post.

We'll start getting Python set up to work through this now (cipher_utils is a simple module with some of the functions I created for my previous cipher-solving post, downloadable from this blog's repo on Gitlab):

%matplotlib inline
import random
import string

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle

from cipher_utils import *

Then we can breed two random keys like:

def crossover(key1, key2, crossover_point=None):
    if crossover_point is None:
        crossover_point = random.randint(0, 25)
    
    child = {}
    available = set(string.ascii_lowercase)
    for x in string.ascii_lowercase[:crossover_point]:
        child[x] = key1[x]
        available.remove(key1[x])
    for x in string.ascii_lowercase[crossover_point:]:
        if key2[x] in available:
            child[x] = key2[x]
        else:
            child[x] = random.choice(list(available))
        available.remove(child[x])
        
    return child

a, b = make_random_key(), make_random_key()
child = crossover(a, b, crossover_point=12)
for key in a, b, child:
    print(''.join(key.values()))

mnhkceigqlvybfspdrzxjotwau
pamsrlibwhtkzfexqdyvungcjo
mnhkceigqlvyzfoxudratbswjp

Why this solution doesn't quite work

The crossover() function above doesn't quite work like our simple example from earlier: the issue is that with this cipher solving problem, once a letter is used in the key we can't use it again. So we take letters from parent 1 up to the crossover point, but when taking letters from parent 2 after the crossover point, we have to check if they've been used yet, and if they have, randomly pick from the letters that are still available. Overall this probably means that we're using elements from parent 2 less often than parent 1, but we can still end up using most of parent 2 when the crossover point is early in the strong.

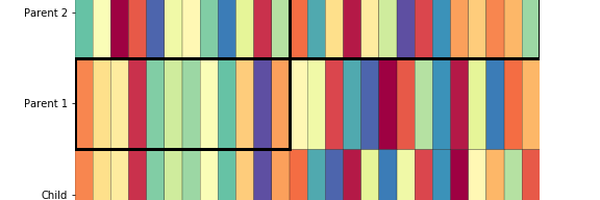
We can also visualize the crossover like:

def key_to_list(k):
    letter_to_num = {letter: i for i, letter in enumerate(string.ascii_lowercase)}
    return [letter_to_num[k[letter]] for letter in string.ascii_lowercase]

def plot_crossover(parent1, parent2, child, crossover_point):  
    key_array = np.array([key_to_list(k) for k in [child, parent1, parent2]])

    fig, ax = plt.subplots()
    fig.set_size_inches(8, 3)
    ax.pcolor(key_array, cmap=plt.cm.Spectral, edgecolors='black')
    box1 = Rectangle((0, 1), width=crossover_point, height=1,
                     fill=False, edgecolor='black', linewidth=3)
    box2 = Rectangle((crossover_point, 2), width=26 - crossover_point, height=1,
                     fill=False, edgecolor='black', linewidth=3)
    ax.add_patch(box1)
    ax.add_patch(box2)
    ax.set_yticks([0.5, 1.5, 2.5])
    ax.set_yticklabels(['Child', 'Parent 1', 'Parent 2'])
    ax.set_ylim(0, 3.1)
    ax.set(frame_on=False)
    
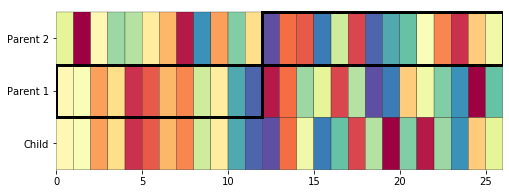
plot_crossover(a, b, child, crossover_point=12)

Applying the solution anyway

It turns out that despite the issues with generating a proper child from two solutions, the genetic algorithm approach still works well enough to solve a substitution cipher, reaching a decent (if not perfect) solution in under 1000 generations.

To help the process along, we'll also allow for mutation: randomly changing the solution by swapping two elements of the key to prevent it getting totally stuck in a local maximum:

def mutate(key):
    a, b = random.choices(string.ascii_lowercase, k=2)
    key[a], key[b] = key[b], key[a]

Once again, we'll encrypt Alice In Wonderland using a random key, and use the letter and bigram frequencies from Frankenstein to score the fitness against:

alice = get_simple_text('alice.txt')
frank = get_simple_text('frank.txt')

encrypt_key = make_random_key()

alice_encrypted = decrypt(alice, encrypt_key)
letter_probs = make_letter_probs(frank)
bigram_probs = make_bigram_probs(frank)
print(alice[1012:1105])
print(alice_encrypted[1012:1105])

the hot day made her feel very sleepy and stupid whether the pleasure of making a daisychain 
pjo jyp zfi sfzo jog xooe logi beooui fkz bptunz cjopjog pjo ueofbtgo yx sfhnkm f zfnbivjfnk 

Running the genetic algorithm

We'll run our genetic algorithm for 1000 generations, generating a population of 10 keys each time. At each generation, we'll breed the top 2 keys to create a new population of 10 keys.

Here's the code I used to do that. I think it works out to be nice and simple (and could be shorter if I left out a couple of tweaks I've addded like mutation):

pop_size = 10
n_generations = 1000
mutation_rate = 1 / 50
population = [make_random_key() for i in range(pop_size)]
best_scores = []

best_fitness = -float("inf")
best_decrypt = None

for gen_num in range(n_generations):
    decrypts = [decrypt(alice_encrypted, k) for k in population]
    fitness = np.array([score_text(txt, letter_probs, bigram_probs) 
                        for txt in decrypts])
    
    if max(fitness) > best_fitness:
        best_fitness = max(fitness)
        best_decrypt = decrypts[fitness.argmax()]
    best_scores.append(max(fitness))
    
    new_generation = []
    # Get parents: the 2 top scoring keys
    p1, p2 = fitness.argsort()[::-1][:2]
    for child_num in range(pop_size):        
        child = crossover(population[p1], population[p2])
        
        # Make the mutation rate 1 if all the keys end up the same
        #  to prevent getting stuck
        do_mutate = random.random() < mutation_rate
        if do_mutate or (fitness.ptp() == 0):
            mutate(child)
        
        new_generation.append(child)
        
    population = new_generation
    
print(decrypts[fitness.argmax()][1012:1105])
print(best_decrypt[1012:1105])

the hot day made her feel jery sleecy and sticud whether the cleasire of maqung a dausyphaun 
the hot day cade her feel very sleepy and stupid xhether the pleasure of caking a daisywhain 

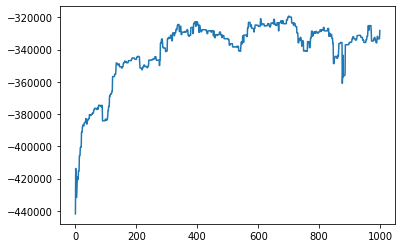
We can see how quickly the algorithm converged on a decent solution, which is much faster than the hill-climbing method I used in the last post. We might even see the algorithm hit a peak and then move away from it, possibly a sign we should be trying to stop the algorithm earlier.

plt.plot(best_scores)

[<matplotlib.lines.Line2D at 0x7f5e43ba2410>]

I'd like to investigate whether there's a way to apply genetic algorithms while avoiding the "used letter" problem, but I think this shows how useful the GA approach can be even in situations where they're an imperfect fit.